경사하강법
4.2 경사 하강법
위와는 아주 다른 방법의 선형 회귀 모델 훈련 방법이다. 경사 하강법gradient descent은 여러 종류의 문제에서 최적의 해법을 찾을 수 있는 일반적인 최적화 알고리즘이다.
- 동작 방식 : 무작위 초기화로 된 임의의 값으로 시작해서 한번에 조금씩 비용 함수가 감소되는 방향으로 진행하여 알고리즘이 최솟값에 수렴할 때까지 점진적으로 향상시킨다.
기본 아이디어 : 비용 함수를 최소화하기 위해 반복해서 파라미터를 조정해가는 것이다.
- 학습 스텝의 크기는 비용함수의 기울기에 비례한다.
학습률

- 중요한 파라미터 : 스텝의 크기 즉, 학습률 $\eta$ 하이퍼파라미터로 결정된다. 학습률이 너무 작으면 알고리즘이 수렴하기 위해 반복을 많이 진행해야 하므로 시간이 오래 걸린다. 학습률이 너무 크면 알고리즘을 더 큰 값으로 발산하게 만들어 적절한 해법을 찾지 못하게 한다.
경사 하강법 문제점

-
무작위 초기화 때문에 알고리즘이 왼쪽에서 시작하면 전역 최솟값보다 덜 좋은 지역 최솟값에 수렴한다.
-
오른쪽부터 시작하면 최적점을 찾기 위해 시간이 오래 걸리고 일찍 멈추게 되어 전역 최솟값에 도달하지 못한다.
-
스케일 문제 : 경사 하강법을 사용할 때는 반드시 모든 특성이 같은 스케일을 갖도록 만들어야 한다. 비용함수는 $\theta$관한 함수이며 입력 특성과 타깃 벡터가 주어지면 $\theta$값의 범위가 정해진다. 가중치 벡터 $\theta$가 특성의 스케일에 영향을 받을 것이고, 그 스케일이 일치하지 않으면 비용 함수는 타원 모양이 된다. 최소값을 찾기까지 오랜 시간이 걸리는 문제가 생긴다.
다행히 MSE 비용 함수는 볼록 함수이기 때문에 하나의 전역 최솟값만 있어서 경사 하강법이 적합하다.
배치 경사 하강법
각 모델 파라미터 $\theta_j$에 대해 비용 함수의 그레이디언트를 계산해야 한다. 이를 편도 함수라고 한다.
비용 함수의 편도함수
$\frac{\partial}{\partial\theta_j}MSE\left(\theta\right) = \frac{2}{m}\sum_{i=1}^m{\left( \mathbf{\theta}^T\mathbf{x}^{(i)}-y^{(i)}\right)x_j^{(i)}}$
벡터로 한꺼번에 계산할 수 있다.
$\nabla_{\theta}MSE(\mathbf{\theta})$
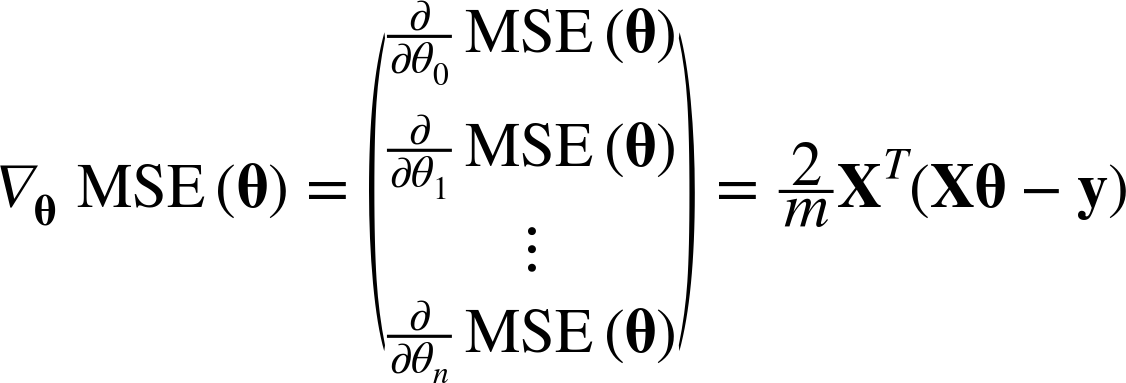
이 공식은 매 경사 하강법 스텝에서 전체 훈련 세트 $\mathbf{X}$에 대해 계산한다. 매 스텝에서 훈련 데이터 전체를 사용한다.(이는 배치 경사 하강법의 단점이 된다.) 그래서 매우 큰 훈련세트에서는 아주 느리다. 하지만 경사 하강법은 특성 수에는 민감하지 않아 수십만 개의 특성에서 선형 회귀를 훈련시키려면 경사하강법이 훨씬 빠른 방법이다.

학습률에 따라 경사 하강법으로 구현되는 것이 달라진다.
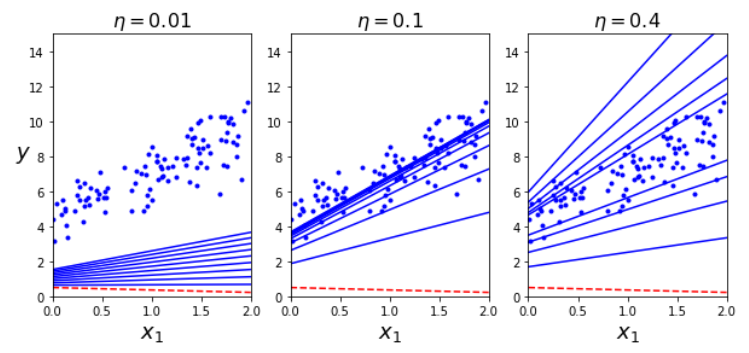
적절한 학습률을 찾으려면 그리드 탐색을 사용한다. 하지만 그리드 탐색에서 수렴하는 데 너무 오래 걸리는 모델을 막기 위해 반복되는 횟수를 제한해야한다.
- 해결책 : 반복 횟수를 아주 크게 정하고 그레이디언트 벡터가 아주 작아지면, 경사 하강법이 최솟값에 도달한 것이므로 알고리즘을 중지한다.
수렴율
비용 함수가 볼록 함수이고 기울기가 급격하게 바뀌지 않는 경우, 학습률을 고정한 배치 경사 하강법은 어느 정도 시간이 걸리겠지만 결국 최적의 솔루션에 수렴할 것이다. 항상 같은 데이터(전체 데이터)에 대해 경사를 구하기 때문에 수렴이 안정적이다. 비용 함수의 모양에 따라 달라지겠지만, $\varepsilon$ 범위 안에서 최적의 솔루션에 도달하기 위해서는 $O\left(1/\varepsilon\right)$의 반복이 걸릴 수 있다. 허용 오차 $\varepsilon$을 1/10로 줄이면 알고리즘의 반복은 10배 늘어난다.
확률적 경사 하강법
배치 경사 하강법의 문제점은 매 스텝마다 전체 훈련 세트를 사용해 그레이디언트를 계산한다는 것이다.
-
동작 방식 : 매 스텝에서 한 개의 샘플을 무작위로 선택하고 그 하나의 샘플에 대한 그레이디언트를 계산한다.
- 특징
- 매 스텝에서 한 개의 샘플을 무작위로 선택한다.
- 장) 매 반복에서 다뤄야 할 데이터가 매우 적기 때문에(한 개의 샘플) 알고리즘이 훨씬 빠르다.
- 장)매 반복에서 한 개의 샘플만 메모리에 있으면 되기 때문에 매우 큰 훈련 세트도 훈련시킬 수 있다.
- 확률적으로 샘플을 선택한다.
- 단) 배치 경사 하강법보다 불안정하다. 비용함수가 최솟값에 다다를 때까지 위아래로 요동치며 평균적으로 감소한다. 좋은 파라미터가 구해지겠지만 최적치는 아닌 값이다. -> [해결방법] 학습률을 점진적으로 감소시킨다.
- 장) 비용 함수가 매우 불규칙 할 때 알고리즘이 지역 최솟값을 건너뛰도록 도와주므로 배치 경사 하강법보다 전역 최솟값을 찾을 가능성이 높다.
- 매 스텝에서 한 개의 샘플을 무작위로 선택한다.
-
학습스케쥴 : 매 반복에서 학습률을 결정하는 함수
- 에폭epoch: 한 반복에서 m번 되풀이 되는데, 이때 각 반복을 에폭이라고 한다.
- 샘플 선택 문제 : 샘플을 무작위로 선택하기 때문에 어떤 샘플은 여러 에폭에서 선택될 수 있고 어떤 샘플은 전혀 선택되지 않을 수 있다.
- 알고리즘이 에폭마다 모든 샘플을 사용하게 하려면 훈련 세트를 섞은 후 차례대로 하나씩 선택하고 다음 에포크에서 다시 섞는 식의 방법을 사용할 수 있다. 하지만 이는 늦게 수렴된다.
- 훈련하는 동안 샘플을 섞는 방법도 있다.
미니배치 경사 하강법
- 동작 방법 : 미니배치(임의의 작은 샘플 세트)에 대해 그레이디언트를 계산한다.
- 장점:
- 행렬 연산에 최적화된 하드웨어, 특히 GPU를 사용해서 얻는 성능 향상
- 미니 배치를 어느 정도 크게 하면 파라미터 공간에서 SGD보다 덜 불규칙하게 움직인다. -> 장) 미니배치 경사 하강법이 SGD보다 최솟값에 더 가까이 도달한다. -> 단) 지역 최솟값에서 빠져나오지는 더 힘들지도 모른다.
