Binary Search Tree
루트 트리(Root Tree)
루트 r을 가진 트리 T에 있는 노드 x를 살펴본다.
- 조상ancestor : r에서 x로 가는 유일한 경로에 있는 임의의 노드 y를 x의 조상이라고 한다. 쉽게 말해서 x 위의 노드들은 조상!
- **자손descendant** : y가 x의 조상이면 x는 y의 자손이다.
- 자식child : x가 y의 자식노드이다.
- 부모parent : y가 x의 부모노드이다.
- 차수 :
- 깊이depth :
- NIL : 노드를 포함하지 않는 이진 트리. 빈 트리, 널 트리 라고도 한다.
이진 검색 트리 자료 구조
트리에 대한 기본 동적 집합 연산들의 평균 수행 시간 : $\theta\left( lg n\right)$
- 특징
- 기본 연산들에 대해서 최악의 경우에도 빠른 실행 속도를 보장할 수 있다.
이진 검색 트리(Binary Search Tree)의 개념
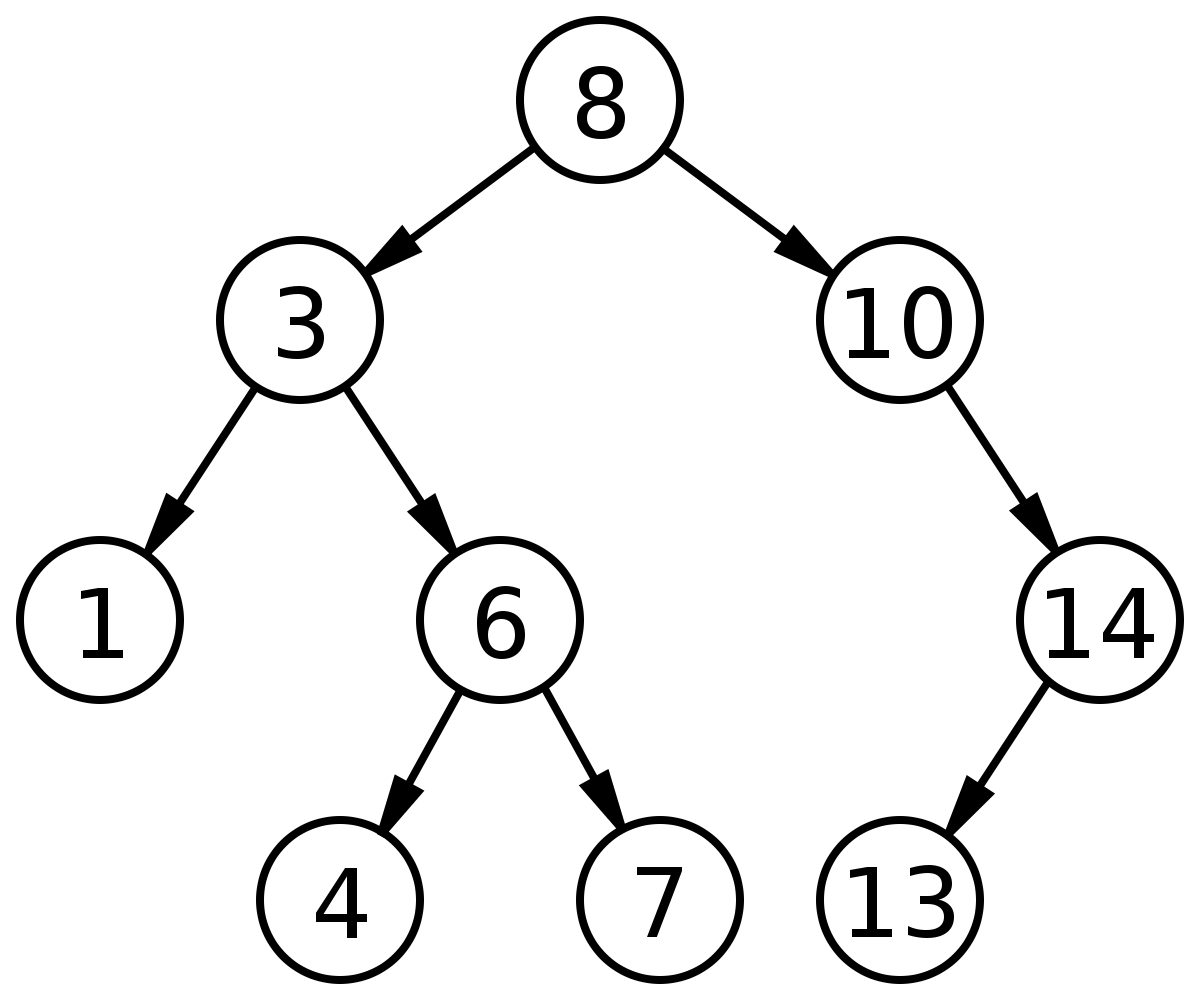
- 개념 : 각 노드를 객체로 하는 연결 자료구조로서, 이진 트리 형태이다. 이진트리와 다른점은 아래의 특성이 없다면 그냥 일반 이진트리이고, 아래 특성이 있다면 이진 검색 트리이다.
- 속성
- key : 트리 T에 속하는 한 노드
- key.right : key의 오른쪽 자식
- key.left : key의 왼쪽 자식
- key.p : key의 부모
-
특성
x를 이진 검색 트리의 한 노드라고 하자. y가 x의 왼쪽 서브 트리의 한 노드면 $y.key \le x.key$ 를 만족한다. 그리고 y가 x의 오른쪽 서브 트리의 한 노드면 $y.key \ge x.key$를 만족한다.
-
- 연산
- 기본적으로 검색, 삽입, 삭제 연산을 수행한다. 검색연산을 먼저 설명하는 이유는 삽입, 삭제 연산에 검색 연산이 사용되기 때문이다.
- $INORDER-TREE-WALK(x)$ : 이진 검색 트리의 모든 키를 정렬된 순서대로 출력한다. 이진 검색 트리 $T$의 모든 원소를 출력하려면 $INORDER-TREE-WALK(T.root)$를 호출하면 된다.
- $TREE-SEARCH(x,k)$ : 이진 검색 트리에서 주어진 키를 가지는 노드를 검색한다.
- $TREE-MINIMUM(x)$ : 이진 검색 트리에서 최소의 키를 가지는 원소를 찾는다.
- $TREE-MAXIMUM(x)$ : 이진 검색 트리에서 최대의 키를 가지는 원소를 찾는다.
- $TREE-SUCCESSOR(x)$ : 이진 검색 트리의 한 노드가 주어졌을 때, 그 노드의 직후 원소를 찾는다.
- $TREE-INSERT(T,z)$ : 새로운 값 $z$를 이진 검색 트리 $T$에 삽입한다.
- $TREE-DELETE(T,z)$ : 이진 검색 트리 $T$에서 노드 $z$를 삭제한다.
- 연산 별 수행 시간 비교
- $n$ : 이진 검색 트리 $T$의 노드 개수
- $h$ : 이진 검색 트리 $T$의 높이
연산 수행시간 비고 $INORDER-TREE-WALK(x)$ $\theta\left(n\right)$ 재귀적으로 두번 자기 호출을 한다. $TREE-SEARCH(x,k)$ $O\left(h\right)$ 트리의 루트로부터 시작되는 하나의 경로를 따라 내려가면서 그 경로의 노드를 만난다. $TREE-MINIMUM(x)$
$TREE-MAXIMUM(x)$$O\left(h\right)$ $TREE-SEARCH(x,k)$와 동일 $TREE-SUCCESSOR(x)$ $O\left(h\right)$ $TREE-SEARCH(x,k)$와 동일 $TREE-INSERT(T,z)$ $O\left(h\right)$ - $TREE-DELETE(T,z)$ $O\left(h\right)$ - - $INORDER-TREE-WALK(x)$ : 입력된 이진 검색 트리의 수열을 출력한다.
- $TREE-SEARCH(x,k)$ : 이진 검색 트리에서 찾고자 하는 key를 찾아 값을 반환한다. k값이 루트 노드보다 크면 오른쪽, 작으면 왼쪽으로 타고 내려가며 찾는다. 만약 k값을 찾는다면 그 값을 반환하고 없다면 그 트리에 k값이 존재하지 않는다는 경고문과 함께 출력한다.
- $TREE-INSERT(T,z)$ : z 값이 입력될 수 있는 위치를 찾는다. 위치를 찾았다면, 그 공간이 비어있는지를 확인하고 list로 그 자리를 만든다. 그리고 값을 할당한다.
- $TREE-DELETE(T,z)$ : z값을 찾아 삭제한다.
- 1) 만약 해당 노드의 자식 노드가 없다면, 부모노드와의 연결을 끊고, 할당된 동적 메모리를 없앤다음 값을 삭제하는 리스트 내 원소 삭제 과정을 거친다.
- 2) 자식 노드가 하나 있다면, 자식노드의 값을 z값과 바꾼다음, 자식 노드를 삭제한다.
- 3) 자식 노드가 두개 있다면, 이진 검색 트리의 특성에 따라 그 다음으로 큰 값으로 교체한 뒤 해당 삭제한다. 직후원소를 찾아(z값의 노드의 오른쪽 서브 트리에서 가장 작은 값)야 한다.
python 코드 구현
class Node: # 이진 트리의 노드로 사용할 class 따로 구현. 같이 할 수도 있지만 따로 구현하는게 한계..
def __init__(self,key):
self.key = key # 이진 검색 트리에서 해당 노드의 key값
self.disconnect() # 초기화에는 왼쪽, 오른쪽, 부모 링크가 none이 되어야 한다.
def disconnect(self):
self.left = None # 값이어야 한다.
self.right = None # 값이어야 한다.
self.parent = None # 값이어야한다.
def __str__(self):
return "{}".format(self.key)
class BinarySearchTree:
def __init__(self):
self.root = None
def TreeSearch(self,x,k):
if x is None:
if self.root is None:
return "<Empty Tree>"
else:
return print("cannot find {}".format(k))
if k == x.key:
return k
elif (k < x.key):
return self.TreeSearch(x.left,k)
else:
return self.TreeSearch(x.right,k)
''' key가 없는 value만 가진 노드를 입력값으로 받는다. 그리고 비교해서 검색한다.
'''
def TreeInsert(self,x,z):
if x is None:
self.root = Node(z)
else:
if x.key == z:
return "동일한 값을 삽입할 수 없습니다."
elif x.key > z:
if x.left is None:
x.left = Node(z)
x.left.parent = x
else:
self.TreeInsert(x.left,z)
else:
if x.right is None:
x.right = Node(z)
x.right.parent = x
else:
self.TreeInsert(x.right,z)
def TreeDelete(self,x,z):
if x is None:
if self.root is None: return print("<Empty Tree>")
else: return print("삭제할 node가 없습니다.")
else:
if x.key == z:
if not x.left and not x.right:
x.disconnect()
x.key = None
elif x.left and not x.right:
x.key = x.left.key
x.left.disconnect()
x.left.key = None
elif not x.left and x.right:
x.key = x.right.key
x.right.disconnect()
x.right.key = None
else:
y = self.TreeMinimum(x.right)
x.key = y.key
y.disconnect()
y.key = None
elif x.key > z:
return self.TreeDelete(x.left,z)
else:
return self.TreeDelete(x.right,z)
def TreeMinimum(self,x):
while x.left is not None:
x = x.left
return x
TreeDelete()가 좀 지저분하긴하다. 그리고 TreeMinimum()없이 TreeDelete()에서 노드가 두개일 때 직후원소노드를 y로 받아 삭제하는 것을 추후 구현해야겠다.